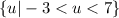Question

Solve this absolute value inequality
8 |u-2| -7<33

Answer 1

In set-builder notation, the set of solutions is:

`\left \u`

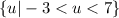
Explanation:

Let's start by isolating the absolute value expression on one side of the inequality:

8 | u - 2 | - 7 < 33

add 7 on both sides:

8 | u - 2 | < 40

divide both sides by 8:

| u - 2 | < 5

Now, in order to remove the absolute value symbols, we need to consider two different cases:

1) what is inside the absolute value symbols is larger than or equal to zero, so in such case when we remove the absolute value we get exactly what was inside:

u - 2 < 5

u < 5 + 2

u < 7

Now the other case;

2) what is inside the absolute value is smaller than zero, then when removing the symbols we get:

2 - u < 5

2 - 5 < u

-3 < u

Then the set of solutions of this inequality are the set of u values such that u is larger than -3 (to the right of -3 on the number line, and smaller than 7 (to the left of the number 7 on the number line.

In graph form this should look like a highlighted segment on the number line that starts at -3 on the left, ends at 7 on the right, and doesn't include the endpoints -3 and 7.

in set builder notation, the set of solutions is given by:

`\left \u`