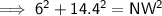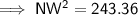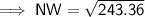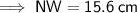Answer:
NW = 15.6 cm
Explanation:
If ΔLMN ~ ΔNWR then:
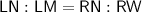
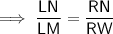
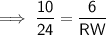
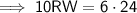
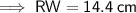
Find NW by using Pythagoras' Theorem:
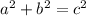
(where a and b are the legs, and c is the hypotenuse, of a right triangle)
Given:
- a = RN = 6 cm
- b = RW = 14.4 cm
- c = NW
Substituting the given values into the formula and solving for NW: