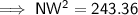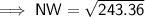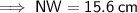Question

Triangles LMN and NWR are right triangles. What is

the length of NW?
24 cm
1.
10 cm
6
>W
R

Answer 1

Find RW then use Pythagorean theorem

• ML/LN=RW/NR
• 24/10=RW/6
• 12/5=RW/6
• 5RW=72
• RW=14.4

So

• NW²=RW²+NR²=6²+14.4²=36+201.6=237.6
• NW=√237.6
• NW=15.5cm

Answer 2

NW = 15.6 cm

Explanation:

If ΔLMN ~ ΔNWR then:

`\sf LN : LM = RN : RW`

`\implies \sf (LN)/(LM)=(RN)/(RW)`

`\implies \sf (10)/(24)=(6)/(RW)`

`\implies \sf 10RW=6 \cdot 24`

`\implies \sf RW = 14.4\:cm`

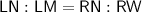
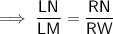
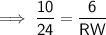
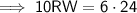
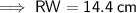
Find NW by using Pythagoras' Theorem:

`a^2+b^2=c^2`

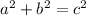
(where a and b are the legs, and c is the hypotenuse, of a right triangle)

Given:

• a = RN = 6 cm
• b = RW = 14.4 cm
• c = NW

Substituting the given values into the formula and solving for NW:

`\implies \sf 6^2+14.4^2=NW^2`

`\implies \sf NW^2=243.36`

`\implies \sf NW=√(243.36)`

`\implies \sf NW=15.6\:cm`