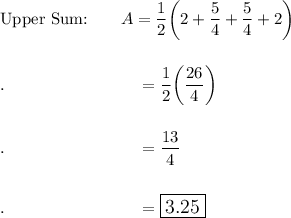Question

How do you do these questions? With step by step instructions please

Answer 1

Answer: n = 3 n = 4

Upper Sum ≈ 3.41 Upper Sum ≈ 3.25

Lower Sum ≈ 2.15 Lower Sum ≈ 2.25

Explanation:

You are trying to find the area under the curve. Area = height x width.

Height is the y-value at the given coordinate --> f(x)

Width is the distance between the x-values --> dx

n = 3

First, let's figure out dx: the distance from -1 to +1 is 2 units. We need to divide that into 3 sections because n = 3 --> dx = 2/3

So the points we will evaluate is when x = {-1, -1/3, 1/3, 1}

For the upper sum, we find the max y-value for each interval

For the lower sum, we find the min y-value for each interval

Next, let's find the height for each of the x-values:

f(x) = 1 + x²

f(-1) = 1 + (-1)² = 2

f(-1/3) = 1 + (-1/3)² = 1 + 1/9 --> 10/9

f(1/3) = 1 + (1/3)² = 1 + 1/9 --> 10/9

f(1) = 1 + (1)² = 2

Interval Max Min

{-1, -1/3} f(-1) = 2 f(-1/3) = 10/9

{-1/3, 1/3} f(-1/3) = 10/9 f(0) = 1 (vertex lies in this interval)

{1/3, 1} f(1) = 2 f(1/3) = 10/9

Now, let's find the Area: A = f(x) dx:

`\text{Upper Sum:}\quad A=(2)/(3)\bigg(2+(10)/(9)+2\bigg)\\\\.\qquad \qquad \qquad =(2)/(3)\bigg((46)/(9)\bigg)\\\\.\qquad \qquad \qquad =(92)/(27)\\\\.\qquad \qquad \qquad =\large\boxed{3.41}`

`\text{Lower Sum:}\qquad A=(2)/(3)\bigg((10)/(9)+1+(10)/(9)\bigg)\\\\\\.\qquad \qquad \qquad \qquad =(2)/(3)\bigg((29)/(9)\bigg)\\\\\\.\qquad \qquad \qquad \qquad =(58)/(27)\\\\\\.\qquad \qquad \qquad \qquad =\large\boxed{2.15}`

*****************************************************************************************

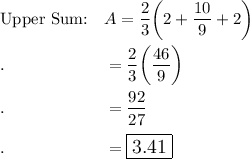
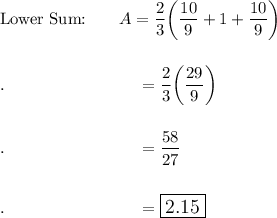
n = 4

First, let's figure out dx: the distance from -1 to +1 is 2 units. We need to divide that into 4 sections because n = 4 --> dx = 2/4 = 1/2 (simplified)

So the points we will evaluate is when x = {-1, -1/2, 0, 1/2, 1}

For the upper sum, we find the max y-value for each interval

For the lower sum, we find the min y-value for each interval

Next, let's find the height for each of the x-values:

f(x) = 1 + x²

f(-1) = 1 + (-1)² = 2

f(-1/2) = 1 + (-1/2)² = 1 + 1/4 --> 5/4

f(0) = 1 + (0)² = 1

f(1/2) = 1 + (1/2)² = 1 + 1/4 --> 5/4

f(1) = 1 + (1)² = 2

Interval Max Min

{-1, -1/2} f(-1) = 2 f(-1/2) = 5/4

{-1/2, 0} f(-1/2) = 5/4 f(0) = 1

{0, 1/2} f(1/2) = 5/4 f(0) = 1

{1/2, 1} f(1) = 2 f(1/3) = 5/4

Now, let's find the Area: A = f(x) dx:

`\text{Upper Sum:}\qquad A=(1)/(2)\bigg(2+(5)/(4)+(5)/(4)+2\bigg)\\\\\\.\qquad \qquad \qquad \qquad =(1)/(2)\bigg((26)/(4)\bigg)\\\\\\.\qquad \qquad \qquad \qquad =(13)/(4)\\\\\\.\qquad \qquad \qquad \qquad =\large\boxed{3.25}`

`\text{Lower Sum:}\qquad A=(1)/(2)\bigg((5)/(4)+1+1+(5)/(4)\bigg)\\\\\\.\qquad \qquad \qquad \qquad =(1)/(2)\bigg((18)/(4)\bigg)\\\\\\.\qquad \qquad \qquad \qquad =(9)/(4)\\\\\\.\qquad \qquad \qquad \qquad =\large\boxed{2.25}`