Complete Question:
A ball is kicked with an initial height of 0.75 meters and initial upward velocity of 22 meters/second. This inequality represents the time, t in
seconds, when the ball's height is greater than 10 meters.
-4.9t² + 22t + 0.75 > 10
The ball's height is greater than 10 meters when t is approximately between __ and __ seconds
Answer:
The ball's height is greater than 10 meters when t is approximately between 0.47 and 4.02 seconds
Explanation:
Given
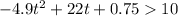
Required
Solve the inequality
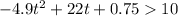
Subtract 10 from both sides
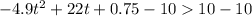
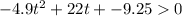
Solve using quadratic formula
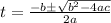
In this case;
a = -4.9; b = 22; c = -9.25
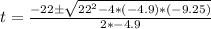
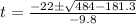
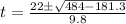
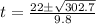
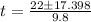
Split
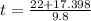 or
or
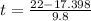
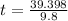 or
or
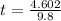
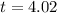 or
or
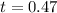
Convert to inequality;
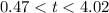
Hence;
The ball's height is greater than 10 meters when t is approximately between 0.47 and 4.02 seconds