Question

Briyana has $150, and she needs to save at least $560 for a spring break trip. If she can save $45 per week, how long will it take her to save enough money? Let w= weeks saving money. Wrote an inequality to describe the situation.

Answer 1

Let's work this out using the inequality it suggests.

We can use the form
`y=mx+b`, but have the equals sign substitute out for whatever sign we need.

When you need to buy something, do you need to have more, less, or the same amount of money to buy something?

You need to have at least the same amount of money.

Which means that we'll be using the ≥ sign.

`y\geq mw+b`

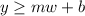
Now let's substitute in some values we know.

She has 150 to start off with, think of this as the y-intercept of the graph.

What variable represents the y-intercept?

You should've said b.

`y\geq mw+150`

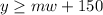
Now how much is she saving her week? $45.

Since this is how much she's saving every week, this represents the slope.

`y\geq 45w+150`

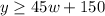
Now, we can solve this plugging in 560 for
`y`, which is how much money she needs.

`560\geq 45x+150`

`410\geq 45w`

`(82)/(9)\geq w`

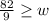
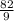`(82)/(9)` is 9.111 (repeating), but we need to round up to the nearest whole number because she probably doesn't deposit money constantly during the week, and rather all at once.

Which means that she needs to save money for 10 weeks to have enough money for the spring break trip.

Hope this helps.

頑張って!

Answer 2

9.1 or 10 weeks

Explanation:

First you need to create an equation: 150 + 45w = 560

You need to get the w by itself. To do this we need to take 150 from both sides: 150 (-150) + 45w = 560 (-150)

45w = 410

Now we have to divide both sides by 45:

w = 9.1

So it took Briyana just over 9 weeks to save $560 for spring break

I hope this helps