Question

Find three consecutive even integers such that when the first integer is

multiplied by the third integer, the result is 2 more than 5 times the
second integer. [Only an algebraic solution will be accepted.]

Answer 1

4, 6, 8

Explanation:

Let the three consecutive integers be a, b, and c.

So, first, we know that they are three consecutive even integers. In other words:

`a=2n,b=2n+2,c=2n+4`

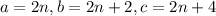
N is any integer, but the 2n ensures that the outcome is even. Since we want to make the subsequent terms also even, we add 2.

We are told that when the first integer (a) is multiplied by the third integer (c), the result is 2 more than 5 times the second integer (b). In other words:

`ac=2+5b`

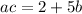
Substitute:

`(2n)(2n+4)=2+5(2n+2)`

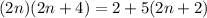
Distribute both sides:

`4n^2+8n=2+10n+10`

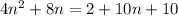
Add on the right:

`4n^2+8n=10n+12`

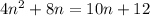
Subtract 10n and 12:

`4n^2-2n-12=0`

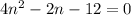
Divide everything by 2:

`2n^2-n-6=0`

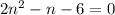
Factor. Find two numbers that when multiplied equals (2)(-6)=-12 and when added equals -1.

3 and -4 works. Thus:

`2n^2-4n+3n-6=0\\2n(n-2)+3(n-2)=0`

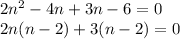
Combine:

`(2n+3)(n-2)=0`

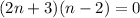
Zero Product Property:

`2n+3=0\text{ or } n-2=0`

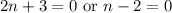
Solve for n:

`n=-3/2\text{ or } n=2`

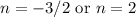
So, n is either -3/2 or 2.

That means that a must be either:

`a=2(-3/2)\text{ or } 2(2)`

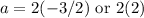
Multiply:

`a=-3\text{ or } 4`

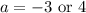
The first answer is not even. So:

`a=4`

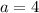
Our first answer is 4.

And our sequence is 4, 6, and 8.

Checking:

4 times 8 is 32.

2 plus 5 times 6 is also 32.

So our answer is correct.