Question

Uncertainty propagation question #2

Hi all, I am trying to calculate the uncertainty and volume for a rectangular block with the measurements being 8.7cm, 5.2cm, 5.4cm. I am struggling with the uncertainty propagation, and I am unsure if I did this correctly. Heres what I've tried.


I found the uncertainty for each individual measurement to be .1 because they all have 1 decimal place. I Added this to the formula with the measurements, took the square root of the sum of the squares with the uncertainty for each individual measurement being in the numerator and the measurement in the denominator, as follows: √(.1/8.7)\^2 + (.1/5.2)\^2 + (.1/5.4)\^2. My final answer was volume= 244.296 +/- .029 cm\^3. I rounded the uncertainty that I got from the equation to 2 significant figures because that’s what the smallest measurement has. Did I do this correctly?

Answer 1

The correct treatment of uncertainties for the volume is shown below

Step-by-step explanation:

In order to estimate the uncertainty in the volume which is derived via the formula:

`V = w*l*h`

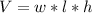
you normally start with the relative errors
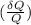`((\delta Q)/(Q))` of each quantity (Q) measured, since they are so easy to handle, stating that the relative error in the Volume is the addition of the relative errors in each quantity:

`(\delta V)/(V) =(\delta w)/(w) +(\delta l)/(l) +(\delta h)/(h)`

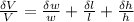
and finally solve for
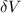`\delta V` by multiplying both sides by the volume you calculated.

In your case, this becomes:

`\delta V =V \left \{(\delta w)/(w) +(\delta l)/(l) +(\delta h)/(h)\right \} \\\delta V = 244.296 \left \{(0.1)/(5.4) +(0.1)/(8.7) +(0.1)/(5.2)\right \}\\\delta V = 244.296 \, (0.04924354)\\\delta V = 12.03 \,\,cm^3`

Then, since the standard practice is to write the uncertainty with ONLY ONE significant figure, the rounding of your uncertainty becomes:

`\delta V=10\,\,cm^3`

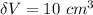
Giving this, you need to express the final measurement as:

`V=240\,\,cm^3\,+/- 10 \,\,cm^3`

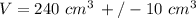
making sure that the expression for the volume doesn't have significant figures passed the limitation imposed by its uncertainty (in this case the tenths).

Please notice as well that in the treatment you did, you:

1) ended up with an uncertainty even smaller than the relative uncertainty of each measurement (which cannot be possible since relative uncertainties add-up)

2) are not rounding your uncertainty to ONE SIG FIG.