Answer:
The answer is "
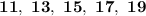 ".
".
Explanation:
In word problem, it is solved by 2k+1, among the most common forms of even an, unlike number.
Let another odd integer become 2k+1.....(a)
(2K+1)+(2k+3)+(2k+5)=(2k+7)+(2k+9)+3(to take the left side 3 extra)
Quality for the k:
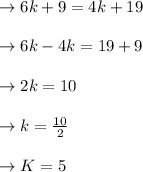
put the value of k, in the equation (a):
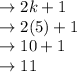
There are also 11, 13, 15, 17, and 19 episodes.
Let's test it! Let's test it. 11+13+15=39
17+ 19 = 36.
So we're right, the first 3 integer numbers are 3 more than the last 2.