Answer:
The minimum thickness of the soap bubble for destructive interference to occur is 225.56 nm.
Step-by-step explanation:
Given;
wavelength of light, λ = 600 nm
The minimum thickness of the soap bubble for destructive interference to occur is given by;
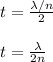
where;
n is refractive index of soap film = 1.33
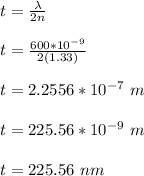
Therefore, the minimum thickness of the soap bubble for destructive interference to occur is 225.56 nm.