Answer:
The maximum height to which water could be squirted with the hose is 13.380 meters.
Step-by-step explanation:
A line of current of a fluid can be explained sufficiently by Bernoulli's Theorem. In this case, the system can be simplified due to neglectance of changes in absolute pressure. Water is squirted with an initial speed and reaches its maximum height, where final speed is zero. That is to say:
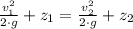
Where:
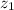 ,
,
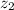 - Initial and final height of water, measured in meters.
- Initial and final height of water, measured in meters.
 - Gravitational acceleration, measured in meters per square second.
- Gravitational acceleration, measured in meters per square second.
 ,
,
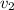 - Initial and final speed of water, measured in meters per second.
- Initial and final speed of water, measured in meters per second.
If
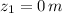 ,
,
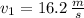 ,
,
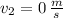 and
and
 , then:
, then:

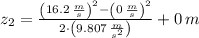
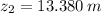
The maximum height to which water could be squirted with the hose is 13.380 meters.