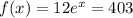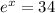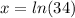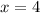Question

Find the average value of the function over the given interval. (Round your answer to three decimal places.) f(x)

Answer 1

Complete Question

Find the average value of the function over the given interval. (Round your answer to three decimal places.) f(x) = 12e^x, [−6, 6] Find all values of x in the interval for which the function equals its average value. (Enter your answers as a comma-separated list. Round your answers to three decimal places.)

Answer:

The average is

`AV  =  403`

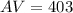
The value of x is

`x =  4`

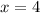
Explanation:

From the question we are told that

The equation is
`f(t) =  12e^x`

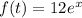
The points consider is [-6 , 6]

Generally the average value of the function over the given interval is mathematically represented as

`AV  =  (1)/(z-w) \int\limits^ z_w {f(x)} \, dx`

`AV  =  (1)/( 6 - (-6))  \int\limits^(6)_(-6) { 12e^x} \, dx`

`AV  =  (1)/(12 ) e^x| \left 6} \atop {-6}} \right.`

`AV  = e^6 -e^(-6)`

`AV  =  403`

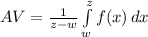
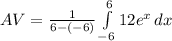
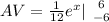
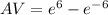
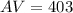
Generally when the function equal the average we have that

`f(x) =  12e^(x) =  403`

`e^(x) =  34`

`x =  ln(34)`

`x =  4`