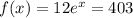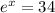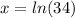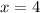Complete Question
Find the average value of the function over the given interval. (Round your answer to three decimal places.) f(x) = 12e^x, [−6, 6] Find all values of x in the interval for which the function equals its average value. (Enter your answers as a comma-separated list. Round your answers to three decimal places.)
Answer:
The average is
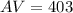
The value of x is
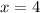
Explanation:
From the question we are told that
The equation is
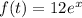
The points consider is [-6 , 6]
Generally the average value of the function over the given interval is mathematically represented as
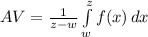
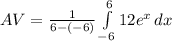
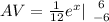
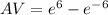
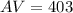
Generally when the function equal the average we have that