Question

A fair die is rolled 72 times and the percentage of 6s is recorded. What is the probability that at most 10% of the rolls are 6s

Answer 1

P (
`\hat p` ≤ 0.10)

Explanation:

The probability in terms of statistics for this given problem can be written as follows.

Let consider X to the random variable that represents the number of 6's in 7 throws of a dice, then:

X
`\sim`Bin ( n = 72, p = 0.167)

E(X) = np

E(X) = 72× 0.167

E(X) = 12.024

E(X)
`\simeq` 12

p+q =1

q = 1 - p

q = 1 - 0.167

q = 0.833

V(X) = npq

V(X) = 72 × 0.167 × 0.833

V(X) = 10.02

V(X)
`\simeq` 10

∴ X
`\sim` N (
`\mu = 12, \sigma^2 =10`)

⇒
`\hat p = (X)/(n) \sim N ( p, (pq)/(n))`

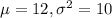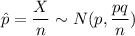
where p = 0.167 and
`(pq)/(n)` =
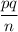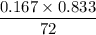`(0.167 * 0.833)/(72)` = 0.00193

∴ P(at most 10% of rolls are 6's)

i.e

P (
`\hat p` ≤ 0.10)