Answer:
The equation of a sphere with endpoints at (4, 1, 6) and (8, 3, 8) is
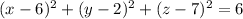 .
.
Explanation:
Given the extremes of the diameter of the sphere, its center is the midpoint, whose location is presented below:
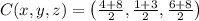
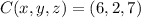
Any sphere with a radius
 and centered at
and centered at
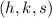 is represented by the following equation:
is represented by the following equation:
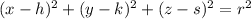
Let be
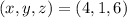 and
and
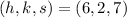 , the radius of the sphere is now calculated:
, the radius of the sphere is now calculated:
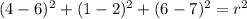
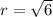
The equation of a sphere with endpoints at (4, 1, 6) and (8, 3, 8) is
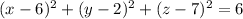 .
.