Question

Find an equation of a sphere if one of its diameters has endpoints (4, 1, 6) and (8, 3, 8).

Answer 1

The equation of a sphere with endpoints at (4, 1, 6) and (8, 3, 8) is
`(x-6)^(2)+(y-2)^(2)+(z-7)^(2) = 6`.

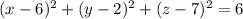Explanation:

Given the extremes of the diameter of the sphere, its center is the midpoint, whose location is presented below:

`C(x,y,z) = \left((4+8)/(2),(1+3)/(2),(6+8)/(2)\right)`

`C(x,y,z) = (6,2,7)`

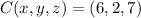
Any sphere with a radius
`r` and centered at
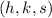`(h,k,s)` is represented by the following equation:

`(x-h)^(2)+(y-k)^(2)+(z-s)^(2) = r^(2)`

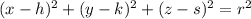
Let be
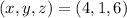`(x,y,z) = (4,1,6)` and
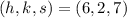`(h,k,s) = (6,2,7)`, the radius of the sphere is now calculated:

`(4-6)^(2)+(1-2)^(2)+(6-7)^(2)=r^(2)`

`r = √(6)`

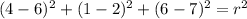
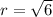
The equation of a sphere with endpoints at (4, 1, 6) and (8, 3, 8) is
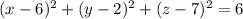`(x-6)^(2)+(y-2)^(2)+(z-7)^(2) = 6`.