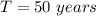Answer:
a.
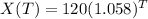
b. Population after 3 years is 142
c. 50 years
Explanation:
Given
Type of growth: Exponential
Initial number of rats = 120
Number of rats (15months) = 280
Solving (a)
Since the growth type is exponential, we make use of the following exponential progression
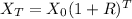
Where Xo is the initial population;
Xo = 125
 is the current population at T month
is the current population at T month
So;
 ; when
; when
Substitute these values in the above formula
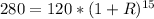
Divide both sides by 120
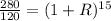
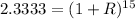
Take 15th root of both sides
![\sqrt[15]{2.3333} =1 + R](https://img.qammunity.org/2021/formulas/mathematics/college/pb402csog50bm3z265suaea244n7ve9ezc.png)
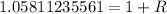
Subtract 1 from both sides
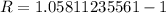
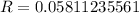
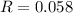 (Approximated)
(Approximated)
Plug in values of R and Xo in
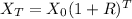
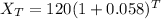
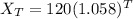
Write as a function
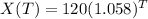
Hence, the function is
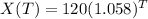
Solving (b):
Population after 3 years
In this case, T = 3
So:
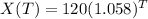
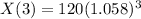
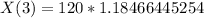
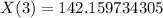
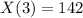 (Approximated)
(Approximated)
Solving (c): When population will reach 2000
Here: X(T) = 2000
So:
So:

Divide both sides by 120
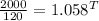
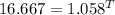
Take Log of both sides
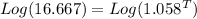
Apply law of logarithm
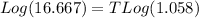
Divide both sides by Log(1.058)
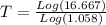
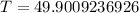
Approximate