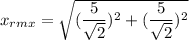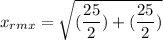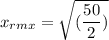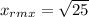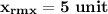Question

Find the power and the rms value of the following signal square: x(t) = 10 sin(10t) sin(15t)

1. Px =
2. xrmx =

Answer 1

`\mathbf{P_x =25 \ watts}`

`\mathbf{x_(rmx) = 5 \ unit}`

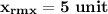
Step-by-step explanation:

Given that:

x(t) = 10 sin(10t) . sin (15t)

the objective is to find the power and the rms value of the following signal square.

Recall that:

sin (A + B) + sin(A - B) = 2 sin A.cos B

x(t) = 10 sin(15t) . cos (10t)

x(t) = 5(2 sin (15t). cos (10t))

x(t) = 5 × ( sin (15t + 10t) + sin (15t-10t)

x(t) = 5sin(25 t) + 5 sin (5t)

From the knowledge of sinusoidial signal Asin (ωt), Power can be expressed as:

`P= (A^2)/(2)`

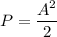
For the number of sinosoidial signals;

Power can be expressed as:

`P = (A_1^2)/(2)+ (A_2^2)/(2)+ (A_3^2)/(2)+ ...`

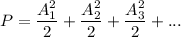
As such,

For x(t), Power
`P_x = (5^2)/(2)+ (5^2)/(2)`

`P_x = (25)/(2)+ (25)/(2)`

`P_x = (50)/(2)`

`\mathbf{P_x =25 \ watts}`

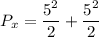
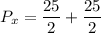
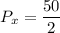
For the number of sinosoidial signals;

`RMS = \sqrt{((A_1)/(√(2)))^2+((A_2)/(√(2)))^2+((A_3)/(√(2)))^2+...`

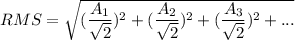
For x(t), the RMS value is as follows:

`x_(rmx) =\sqrt{((5)/(√(2)) )^2 +((5)/(√(2)) )^2 }`

`x_(rmx )=\sqrt{((25)/(2) ) +((25)/(2) ) }`

`x_(rmx )=\sqrt{((50)/(2) )}`

`x_(rmx) =√(25)`

`\mathbf{x_(rmx) = 5 \ unit}`