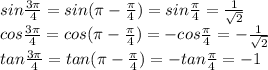Answer:
Explanation:
Before we can determine the exact trigonometric ratios for the angle x whose radian measure is given as
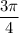 , we need to first determine the quadrant the angle falls into.
, we need to first determine the quadrant the angle falls into.
The angle
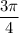 =
=
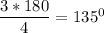 and it falls in the second quadrant. since the angle is positive, we will use the trigonometry ratio that is positive in the second quadrant. The trigonometry ratio that is positive in the second quadrant is sin(x) while others are negative.
and it falls in the second quadrant. since the angle is positive, we will use the trigonometry ratio that is positive in the second quadrant. The trigonometry ratio that is positive in the second quadrant is sin(x) while others are negative.