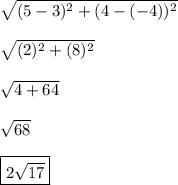Answer:
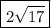
Explanation:
To find the distance between two points, we use the distance formula. The distance formula is:
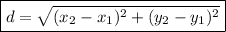
Therefore, we can label our coordinate pairs and solve for d.
Because we are given two coordinate pairs, we will follow the standard naming system for coordinate pairs. This is
 . Therefore, we can implement the distance formula and solve.
. Therefore, we can implement the distance formula and solve.