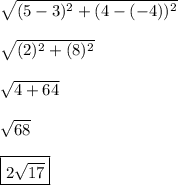Question

20 POINTS !!!

Find the distance between the points (3,-4) and (5, 4)

Answer 1

`d=2√(17)\approx8.2462`

Explanation:

To find the distance between two points, use the distance formula.

The distance formula is:

`d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2`

Let (3,-4) be x₁ and y₁ and let (5,4) be x₂ and y₂. Therefore:

`d=\sqrt{(5-3)^2+(4--4)^2`

Simplify:

`d=\sqrt{(2)^2+(8)^2`

Square:

`d=√(4+64)`

Add:

`d=√(68)`

Simplify:

`d=√(4\cdot17)=\sqrt4\cdot√(17)`

Simplify:

`d=2√(17)\approx8.2462`

Answer 2

`\boxed{2√(17)}`

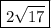
Explanation:

To find the distance between two points, we use the distance formula. The distance formula is:

`\boxed{d=\sqrt{(x_(2)-x_(1))^(2)+({y_(2)-y_(1))^(2)}}}`

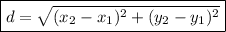
Therefore, we can label our coordinate pairs and solve for d.

Because we are given two coordinate pairs, we will follow the standard naming system for coordinate pairs. This is
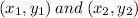`(x_(1), y_(1)) \text \: {and} \: (x_(2), y_(2))`. Therefore, we can implement the distance formula and solve.

`\sqrt{(5-3)^(2)+(4-(-4))^(2)}\\\\\sqrt{(2)^(2)+(8)^(2)}\\\\√(4 + 64) \\\\√(68) \\\\\boxed{2√(17) }`