Question

If we list all the natural numbers below 10 that are multiples of 3 or 5, we get 3, 5, 6 and 9. The sum of these multiples is 23.Find the sum of all the multiples of 3 or 5 below 1000.

Answer 1

Given :

All the natural numbers below 1000 that are multiples of 3 or 5 .

To Find :

The sum of all the multiples of 3 or 5 below 1000.

Solution :

Max multiple of 3 is 999 .

Max multiple of 5 id 995 .

So , number of multiple of 3 is :

`999=a+(n-1)d\\\\999=3+3(n-1)\\\\n=333`

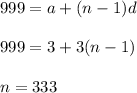
Similarly for 5 .

`995=a+(n-1)d\\\\995=5+5(n-1)\\\\n=199`

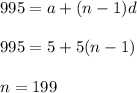
Now , sum of all multiple of 3 is given by :

`S_3=(n)/(2)(2a+(n-1)d)\\\\S_3=(333* (2* 3+332* 3))/(2)\\\\S_3=166833`

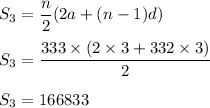
Also , sum of all multiple of 5 is :

`S_5=(n)/(2)(2a+(n-1)d)\\\\S_5=(199* (2* 5+198* 5))/(2)\\\\S_5=99500`

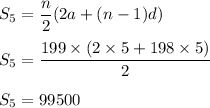
Therefore , total sum :

`T=S_3+S_5\\\\T=166833+99500\\\\T=266333`

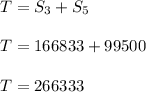
Now , there are some common number which we add two times like :

15 , 30 , 60 ......

So , we should subtract the sum of all multiple of 15 from T .

Now , sum of all multiple of 15 is 33165 .

So ,

`T=266333-33165\\\\T=233168`

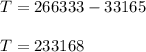
Therefore , the sum of all the multiples of 3 or 5 below 1000 is 233168 .