Given :
All the natural numbers below 1000 that are multiples of 3 or 5 .
To Find :
The sum of all the multiples of 3 or 5 below 1000.
Solution :
Max multiple of 3 is 999 .
Max multiple of 5 id 995 .
So , number of multiple of 3 is :
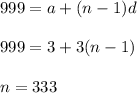
Similarly for 5 .
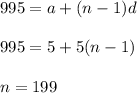
Now , sum of all multiple of 3 is given by :
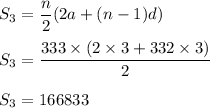
Also , sum of all multiple of 5 is :
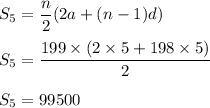
Therefore , total sum :
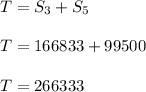
Now , there are some common number which we add two times like :
15 , 30 , 60 ......
So , we should subtract the sum of all multiple of 15 from T .
Now , sum of all multiple of 15 is 33165 .
So ,
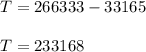
Therefore , the sum of all the multiples of 3 or 5 below 1000 is 233168 .