Answer:
A
Explanation:
So we want an equation that is parallel to:
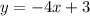
And passes through:
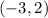
First, since we want the equation to be parallel to the first, the slope must be -4. This is because parallel lines have the same slope.
Now that we know the slope of our equation is -4, we can use the point-slope form to figure out the rest.
The point-slope form is:
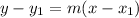
m is -4. Let (-3,2) be x₁ and y₁. Thus:
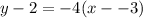
Simplify:
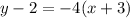
Distribute:
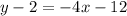
Add 2 to both sides:
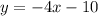
So our answer is A :)