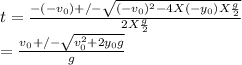Question

For a quadratic function that models the height above ground of a projectile, how do you determine the maximum height or the time when the projectile reaches the ground?

Answer 1

a. y(t) = - 1/2gt² + y₀ b.
`t = \frac{v_(0) +/- \sqrt{v_(0) ^(2) + 2 y_(0)g } }{g }`

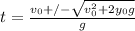
Explanation:

Let the quadratic function y(t) = v₀t - 1/2gt² + y₀ represent the quadratic function that models the height above the ground of the projectile.

a. Maximum Height

At maximum height, the velocity, v₀ = 0, so substituting v₀ = 0 into the equation, we have

y(t) = v₀t - 1/2gt² + y₀

y(t) = 0 × t - 1/2gt² + y₀

y(t) = 0 - 1/2gt² + y₀

y(t) = - 1/2gt² + y₀

b. Time when the projectile reaches the ground

The time when the projectile reaches the ground is gotten when y(t) = 0, So

y(t) = v₀t - 1/2gt² + y₀

0 = v₀t - 1/2gt² + y₀

re-arranging, we have

1/2gt² - v₀t - y₀ = 0

Using the quadratic formula,

`t = \frac{-(-v_(0)) +/- \sqrt{(-v_(0)) ^(2) - 4 X (-y_(0)) X(g)/(2) } }{2 X (g)/(2) } \\= \frac{v_(0) +/- \sqrt{v_(0) ^(2) + 2 y_(0)g } }{g }`