Answer:
![{g}^( - 1) (x) = \sqrt[5]{ - x - 3}](https://img.qammunity.org/2021/formulas/mathematics/college/2v1www8f5ns5wqod9ajzdg0jb6pae3ndiv.png)
Explanation:

To find the inverse of g(x) equate g(x) to y
That's
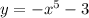
Next interchange the terms
x becomes y and y becomes x
We have
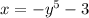
Next make y the subject
Multiply both sides by - 1
That's
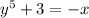
Send 3 to the right side of the equation
That's
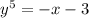
Find the 5th root of both sides
That's
![\sqrt[5]{ {y}^(5) } = \sqrt[5]{ - x - 3} \\ y = \sqrt[5]{ - x - 3}](https://img.qammunity.org/2021/formulas/mathematics/college/yeqse1wtsj7nzskx1xxfdlshk7w9a00gts.png)
We have the final answer as
![{g}^( - 1) (x) = \sqrt[5]{ - x - 3}](https://img.qammunity.org/2021/formulas/mathematics/college/2v1www8f5ns5wqod9ajzdg0jb6pae3ndiv.png)
Hope this helps you