Question

Inverse of g(x)=-x^5-3

Answer 1

`{g}^( - 1) (x) = \sqrt[5]{ - x - 3}`

Explanation:

`g(x) = - {x}^(5) - 3`

To find the inverse of g(x) equate g(x) to y

That's

`y = - {x}^(5) - 3`

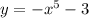
Next interchange the terms

x becomes y and y becomes x

We have

`x = - {y}^(5) - 3`

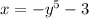
Next make y the subject

Multiply both sides by - 1

That's

`{y}^(5) + 3 = - x`

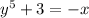
Send 3 to the right side of the equation

That's

`{y}^(5) = - x - 3`

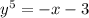
Find the 5th root of both sides

That's

`\sqrt[5]{ {y}^(5) } = \sqrt[5]{ - x - 3} \\ y = \sqrt[5]{ - x - 3}`

We have the final answer as

`{g}^( - 1) (x) = \sqrt[5]{ - x - 3}`

Hope this helps you