Question

The angle of elevation of the top of a tower from a point 100m away is 45 degrees. What is the height of the tower to the nearest metres?​

Answer 1

`\Huge \boxed{\mathrm{100 \ meters}}`

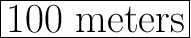
Explanation:

The base of the right triangle created is 100 meters.

The angle between the base and the hypotenuse of the right triangle is 45 degrees.

We can use trigonometric functions to solve for the height of the tower.

`\displaystyle \mathrm{tan(\theta)=(opposite)/(adjacent) }`

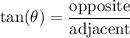
Let the height be x.

`\displaystyle \mathrm{tan(45)}=(x)/(100)`

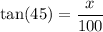
Multiplying both sides by 100.

`\displaystyle 100 \cdot \mathrm{tan(45)}=x`

`100=x`

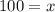
The height of the tower is 100 meters.

Answer 2

SOHCAHTOA.

TOA=opposite/adjacent.

Tan45=100/h.

h tan45=100.

h×1=100.

h=100m