Question

If m∠JKM = 43, m∠MKL = (8 - 20), and m∠JKL = (10x - 11), find each measure.

1. x = ?

2. m∠MKL = ?

3. m∠DEF = ?​

Answer 1

Correct Question: If m∠JKM = 43, m∠MKL = (8x - 20), and m∠JKL = (10x - 11), find each measure.

1. x = ?

2. m∠MKL = ?

3. m∠JKL = ?

Answer/Step-by-step explanation:

Given:

m<JKM = 43,

m<MKL = (8x - 20),

m<JKL = (10x - 11).

Required:

1. Value of x

2. m<MKL

3. m<JKL

Solution:

1. Value of x:

m<JKL = m<MKL + m<JKM (angle addition postulate)

Therefore:

`(10x - 11) = (8x - 20) + 43`

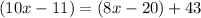
Solve for x

`10x - 11 = 8x - 20 + 43`

`10x - 11 = 8x + 23`

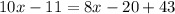
Subtract 8x from both sides

`10x - 11 - 8x = 8x + 23 - 8x`

`2x - 11 = 23`

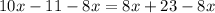
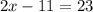
Add 11 to both sides

`2x - 11 + 11 = 23 + 11`

`2x = 34`

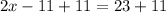
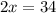
Divide both sides by 2

`(2x)/(2) = (34)/(2)`

`x = 17`

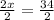
2. m<MKL = 8x - 20

Plug in the value of x

m<MKL = 8(17) - 20 = 136 - 20 = 116°

3. m<JKL = 10x - 11

m<JKL = 10(17) - 11 = 170 - 11 = 159°