Question

A drone carrying fireworks is launched from a platform above a lake and follows a parabolic path. It will set off the fireworks at its highest point. The drone’s height above the surface of the lake is given by the function h(t) = -16t2 + 64t + 80, where h represents height in feet and t represents time in minutes. a. How high is the platform? b. From what height will the fireworks be released? c. When does the drone land?

Answer 1

Yes it is true that’s the answer

Answer 2

Answer: Answer is in the steps

Explanation:

using the function h(t) = -16t^2 + 64t + 80 and H is height in feet t is the time in minutes we can evaluate how high the platform is by solving for the y intercept.

h(t) = -16t^2 + 64t + 80 the y intercept is when h(t) is h(0) so when it is h of zero put zero into the function and solve the function

A) -16(o)^2 + 64(0) + 80

0 -0 + 80

h(0) = 80

Which means the platform is 80 feet high.

B) In the reading it says that it will set the firework at its highest point and in other words its highest point is its vertex. So solve for the vertex .

h(t) = -16t^2 +64t + 80 To solve for the vertex, use the formula x= -b/2a to find the x coordinate of the vertex.

so the value of b is 64 and a is -16 .

x = -64 / -32

x = 2

So the x coordinate of the vertex is 2 so input it and solve for the y coordinate of the vertex.

h(t) = y = -16(2)^2 + 64t+80

y= -16(4) + 64(2)+ 80

y= -64 + 128 + 80

y = 144

So the y coordinate is 144. which means the vertex is (2,144) and also means that the fireworks will be released at a 144 feet.

C) The drone will land on the ground when they is not height which means when y is equal to zero or h(t) is zero.

-16t^2 +64t + 80 = 0 so solve for t using the quadratic formula.

The quadratic formula says that x= -b ±
`√(b^2 -4ac) /2a`

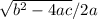
a = -16 b= 64 and c= 80

x = -64 +
`√(9216)/ -32`

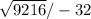
x= -64 ± 96 /-32

x= -1 or x = 5

Which means the drone land on the ground in 5 minutes. It can't be -1 because a negative number can't represent time.