Question

Please I don’t understand this thank you

Answer 1

55°

Explanation:

What we have are vertical angles. Vertical angles are angles directly opposite to one another.

Importantly, the measures of vertical angles are equivalent. Thus, set the expressions to each other and solve for x:

`3x+34=7x+6`

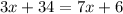
Subtract 3x from both sides:

`34=4x+6`

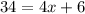
Subtract 6 from both sides:

`28=4x`

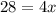
Divide everything by 4:

`7=x`

Flip:

`x=7`

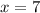
Now, substitute this back into either of the equations since we know they are the same:

`3x+34\\=3(7)+34`

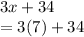
Multiply:

`=21+34`

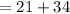
Add:

`=55`

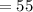
So, the angle is 55°