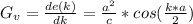Question

The phase velocity of transverse waves in a crystal of atomic separation a is given byy = csin(ka/2) pka/2 1. What is the dispersion relation e(k)? 2. What is the group velocity as a function of k?

Answer 1

a

e(k) = \frac{2a}{c} * sin (\frac{k*a}{2} )

b

G_{v} = \frac{d e(k ) }{dk } = \frac{a^2}{c} * cos (\frac{k* a}{2} )

Step-by-step explanation:

From the question we are told that

The velocity of transverse waves in a crystal of atomic separation is

`b_y  = c (sin ((k*a)/(2) ))/((k*a)/(2) )`

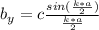
Generally the dispersion relation is mathematically represented as

`e(k) =  b_y  *  k`

=>
`e(k) = c  (sin((k*a)/(2) ) )/( (k*a)/(2) )  *  k`

=>
`e(k) =   c *  (sin ((k_a)/(2) ))/( (a)/(2) )`

=>
`e(k) =  (2a)/(c)  *  sin ((k*a)/(2) )`

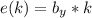
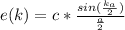
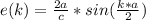
Generally the group velocity is mathematically represented as

`G_(v) =  (d e(k ) )/(dk )  =  (a^2)/(c)  *  cos ((k* a)/(2) )`