Answer:
D. {-3, and -2.5}
Explanation:
Using the quadratic equation, you can find the solution to 2x2+15=-11x.
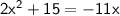
First, you have to add by 11x from both sides.
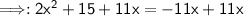
Solve.
2x²+11x+15=0
Use the quadratic formula.
Quadratic formula:
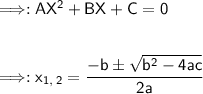
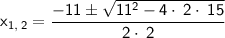
Solve.
Use the order of operations.
PEMDAS
- Parentheses
- Exponents
- Multiply
- Divide
- Add
- Subtract

Multiply the numbers from left to right.
4*2*15=120
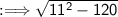
Do exponents.
11²=11*11=121
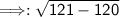
Subtract the numbers from left to right.
121-120=1
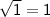
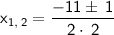
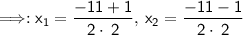
Solve.
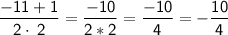
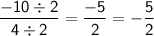
Divide is another options.
-5/2=-2.5
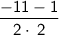
Solve.
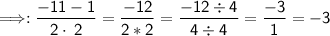
Solutions:
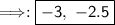
- Therefore, the correct answer is "D. {-3, -2.5}".
I hope this helps. Let me know if you have any questions.