Answer:
The answer is "
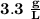 "
"
Step-by-step explanation:
If the endogenous metabolic rate wasn’t substantial after, which
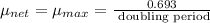 .
.
Throughout the calculating of doubling the time is set at 6.5 hours, consequently

Know we calculate the two-equation,
Initially, the maximum dilution frequency for
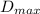 that is:
that is:
![D_(max)= \mu _(max)* \frac{[S_0]}{{K_s + [S_0]}} .....(a)](https://img.qammunity.org/2021/formulas/engineering/college/8ayxechlvo4x0h99evdecpquoyxx762xbt.png)
In secondary the steady concentration of state cells X,
![X = \frac{Y_{(x)/(s)} (s[S_0]-K_sD)}{(\mu _(max)-D)}...... (b)](https://img.qammunity.org/2021/formulas/engineering/college/9z8ugyo4xlqs4sxjcwm1wy5koo098kg0gc.png)
In this section, we will display the
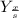 , that is equal to
, that is equal to
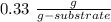 , and the value of the
, and the value of the
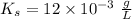 .
.
For equation (a):
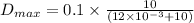
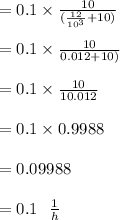
In the Operating value is equal to
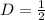 of
of
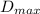 , so D is =
, so D is =
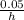 in our case.
in our case.
Finally, the amount of protozoa cells in equation (b):
