Question

Please someone help me. It's about proving related to transformation of trigonometric ratios. Thank you!!​

Answer 1

see explanation

Explanation:

Using sum to product identities

cos x - cos y = - 2sin(
`(x+y)/(2)` )sin(
`(x-y)/(2)` ) = 2sin(
`(x+y)/(2)` )sin(
`(y-x)/(2)` )

cos x + cos y = 2cos(
`(x+y)/(2)` )cos(
`(x-y)/(2)` )

Note that

sin10° = sin(90 - 10)° = cos80°

Thus

`(2sin((10+80)/(2))sin((80-10)/(2)) )/(2cos((10+80)/(2))cos((80-10)/(2)) )` ← cancel 2 from numerator/ denominator

=
`(sin45)/(cos45)` ×
`(sin35)/(cos35)`

= tan45° × tan35° { tan45° = 1 ]

= 1 × tan35°

= tan35° ← as required

Answer 2

Answer: see proof below

Explanation:

* Use the following Co-function Identity: sin A = cos(90 - A)

* Use the following Sum to Product Identities:

cos x - cos y = 2 sin [(x + y)/2] · sin [(x - y)/2]

cos x + cos y = 2 cos [(x + y)/2] · cos [(x - y)/2]

* Use the Unit Circle to evaluate cos 45 = sin 45 = √2/2

Proof LHS → RHS

`\text{LHS:}\qquad \qquad \qquad \qquad \quad (\cos 10-\sin 10)/(\cos 10+\sin 10)\\\\\\\text{Co-function Identity:}\qquad (\cos 10 -\cos (90-10))/(\cos 10+\cos (90-10))\\\\\\\text{Product to Sum Identity:}\quad (2\sin ((10+80)/(2))\sin ((80-10)/(2)))/(2\cos ((10+80)/(2))\cos ((80-10)/(2)))\\\\\\\text{Simplify:}\qquad \qquad \qquad \qquad (2\sin (45)\sin (35))/(2 \cos (45)\cos (35))`

`.\qquad \qquad \qquad \qquad \qquad = (2((\sqrt2)/(2)) \sin (35))/(2((\sqrt2)/(2)) \cos(35))\\\\\\.\qquad \qquad \qquad \qquad \qquad = \tan (35)`

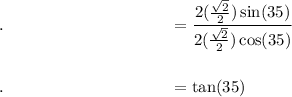
LHS = RHS: tan 35 = tan 35
`\checkmark`