Answer: see proof below
Explanation:
* Use the following Co-function Identity: sin A = cos(90 - A)
* Use the following Sum to Product Identities:
cos x - cos y = 2 sin [(x + y)/2] · sin [(x - y)/2]
cos x + cos y = 2 cos [(x + y)/2] · cos [(x - y)/2]
* Use the Unit Circle to evaluate cos 45 = sin 45 = √2/2
Proof LHS → RHS

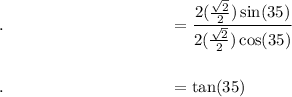
LHS = RHS: tan 35 = tan 35