Question

`x {2} = (25)/(144)`
I don't understand at all​

Answer 1

Explanation:

Hey, there!!

Let me explain you very simply, ok.

Here, according to the question,

`{x}^(2) = (25)/(144)`

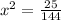
X is square so, which finding the value of x you must take it to the right side (in root form ). so,

`x = \sqrt{ (25)/(144) }`

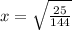
Now, as we know that,

sq.root of 25 = 5

sq.root of 144 = 12

Now, you write it as,

`x = \sqrt{ \frac{ {5}^(2) }{ {12}^(2) } }`

`or \: x = \sqrt{( { (5)/(12) )}^(2) }`

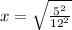
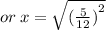
Now, square root and (5/12) square ( square root , square gets cancelled).

You will get as,

`x = (5)/(12)`

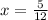
And its your simplified answer.

Hope it helps...