Answer:
AB = 18.8 units
Explanation:
If there are two points (x1,y1) and (x2,y2) on the coordinate plane.
distance between those two points =
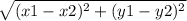
given points are
A= (-4,7)
B= (-12, -10)
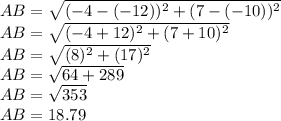
Thus, length of AB is 18.79 units
since, value of hudredth of unit is 9 which is greater than 9 then rounding the value to nearest tenth of unit we increase the value at tenth of unit place by that is 7 becomes 8
length of AB to the nearest tenth of a unit is 18.9 units