Question

Suppose that a box contains 6 cameras and that 3 of them are defective. A sample of 2 cameras is selected at random. Define the random variable X as the number of defective cameras in the sample.

Answer 1

a.

The probability of X

k P(X=k)

0 0.25

1 0.5

2 0.25

b. The expected variable value of X; E(X) = 1

Explanation:

Given that:

number of cameras = 6

numbers of defective = 3

the probability of defective camera p = 3/6 = 0.5

sample size n = 2

Then X = {0,1,2}

Suppose X is the given variable that represents the number of defective cameras in the sample.

∴

X
`\sim` Bin (n =2, p = 0.5)

The probability mass function of binomial distribution can be computed as :

`P(X =x) = (^n_x) p^x (1-p)^(n-x)`

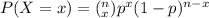
For ;

x = 0

The probability P(X=0)
`= (^2_0) 0.5^0 (1-0.5)^(2-0)`

`P(X=0) = (2!)/(0!(2-0)!) * 1 * 0.5^2`

`P(X=0) =1* 1 * 0.25`

`P(X=0) = 0.25`

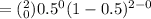
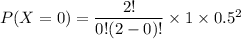
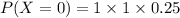
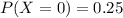
For :

x = 1

The probability P(X=1)
`= (^2_1) 0.5^1 (1-0.5)^(2-1)`

`P(X=1) = (2!)/(1!(2-1)!) * 0.5^1 * 0.5^1`

`P(X=1) =2 * 0.5 * 0.5`

`P(X=1) =0.5`

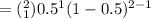
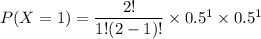
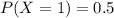
For :

x = 2

The probability P(X=2)
`= (^2_2) 0.5^2 (1-0.5)^(2-2)`

`P(X=2) = (2!)/(2!(2-2)!) * 0.5^2 * 0.5^0`

`P(X=2) =1 * 0.5^2 * 1`

`P(X=2) =0.25`

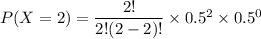
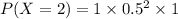
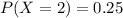
The probability of X

k P(X=k)

0 0.25

1 0.5

2 0.25

The expected variable value of X can be computed as:

E(X) = np

E(X) = 2 × 0.5

E(X) = 1

Answer 2

Answer: 1/5, 1/2, 0.

Explanation:

given data:

no of cameras = 6

no of cameras defective = 3

no of cameras selected = 2

Let p(t):=P(X=t)

p(2)=m/n,

m=binomial(3,2)=3!/2!= 3

n=binomial(6,2)=6!/2!/4! = 15

p(3)= 3/15

= 1/5.

p(1)=m/n,

m=binomial(6,1)*binomial(2,2)=6!/1!/4!*2!/2!/0!= 7.5

n=binomial(6,2)= 15

p(2)= 7.5/15

= 1/2

p(0)=m/n,

m=0

p(0)=0