Question

MDM4U

11. Avery and Bradley work at a large electronics manufacturer that produces DVD players. The
defective rate on the assembly line has gone up to 12% and the manager wants to know the
probability that a skid of 50 DVD players will contain at least 3 defective units.
a) Help Avery use the binomial distribution P(x)=, C.pqrs to answer this question

Answer 1

0.9487

Explanation:

a) The probability of having a defective product = p = 12% = 0.12

The probability of not having a defective product = q = 1 - p = 1 - 0.12 = 0.88

The number of DVD players = n = 50

X is the number of defective products.

The probability that a skid of 50 DVD players will contain at least 3 defective units = P(X ≥ 3) = 1 - P(X ≤ 2)

P(X ≤ 2) = P(X = 0) + P(X = 1) + P(X = 2)

Using binomial:

P(X = 0) =
`C(n,x)p^xq^(n-x)=C(50,0)p^0q^(50-0)=(50!)/((50-0)!0!)*0.12^0*0.88^(50-0)=0.0017`

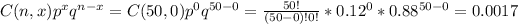
P(X = 1) =
`C(n,x)p^xq^(n-x)=C(50,1)p^1q^(50-1)=(50!)/((50-1)!1!)*0.12^1*0.88^(50-1)=0.0114`

P(X = 2) =
`C(n,x)p^xq^(n-x)=C(50,2)p^2q^(50-2)=(50!)/((50-2)!2!)*0.12^2*0.88^(50-2)=0.0382`

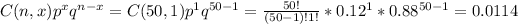
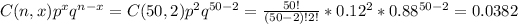
P(X ≤ 2)= 0.0017 + 0.0114 + 0.0382 = 0.0513

P(X ≥ 3) = 1 - P(X ≤ 2) = 1 - 0.0513 = 0.9487 = 94.87%