Answer:
Explanation:
Let be
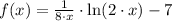 , the first and second derivatives of the function are, respectively:
, the first and second derivatives of the function are, respectively:
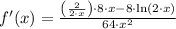
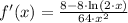
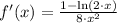
![f''(x) = (\left(-(2)/(2\cdot x) \right)\cdot (8\cdot x^(2))-[1-\ln(2\cdot x)]\cdot (16\cdot x))/(64\cdot x^(4))](https://img.qammunity.org/2021/formulas/mathematics/college/mqaav9ftnzfelxvb6nqi4ki1d7dj1ky9b6.png)
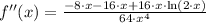

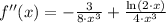
Now, let equalise the first derivative to zero and solve the resulting expression:
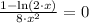
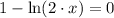

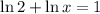
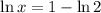
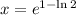
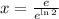

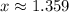
This result is evaluated at the second derivative expression:
![f''(1.359) =-(3)/(8\cdot (1.359)^(3))+(\ln [2\cdot (1.359)])/(4\cdot (1.359)^(3))](https://img.qammunity.org/2021/formulas/mathematics/college/e9fnel6ea904vg8a25in19ri6h43dm9hn3.png)
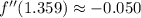
The critical value leads to a critical maximum and there are two intervals:
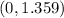 - Increasing
- Increasing
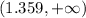 - Decreasing
- Decreasing
The graphic of the function is presented below as attachment.