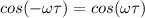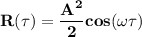Answer:
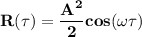
Explanation:
To find Autocorrelation function of the following periodic function
Given that:
X(t) = A sin(wt +θ)
with the period T=2π/w , A, θ, and w are constants.
The autocorrelation function of periodic function with period and phase θ can be expressed as:
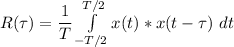
![R(\tau) = (A^2)/(T) \int \limits ^(T/2)_(-T/2) \ A sin ( \omega t + \theta)*A sin [ \omega (t- \tau ) + \theta] \ dt](https://img.qammunity.org/2021/formulas/mathematics/college/xf5v5szye53gucsoei4fvlgttnyggzeu3y.png)
where;
![sinAsin B = (1)/(2)[cos (A-B) -cos (A+B)]](https://img.qammunity.org/2021/formulas/mathematics/college/s4i9ruvgzq82qk30kfaxb728y3avei3bs6.png)
Then;
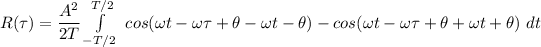
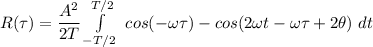
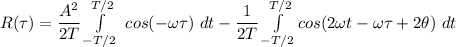
The term 2 is the cosine wave of frequency and the phase =
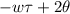
if we integrate that, the second term in the expansion for R(t) = zero
As such,
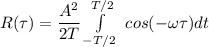
where ;
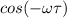 is constant
is constant
Then :
![R(\tau) = (A^2)/(2T) cos (-\omega \tau) [t]^(T/2)_(-T/2)](https://img.qammunity.org/2021/formulas/mathematics/college/z7ph4l49ivx06sdjyhuyyeubyekov91xe2.png)
![R(\tau) = (A^2)/(2T) cos (-\omega \tau) * [(T)/(2)+ (T)/(2)]](https://img.qammunity.org/2021/formulas/mathematics/college/kk4qvlvdezov2n4nefl3zazw9rmxt5lme9.png)
![R(\tau) = (A^2)/(2T) cos (-\omega \tau) * [(2T)/(2)]](https://img.qammunity.org/2021/formulas/mathematics/college/oe9xus2xjutb8g8rs4osxqe84lbabvfaut.png)
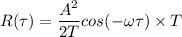
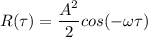
since