Answer:
a turkey at the farm which weighs more than 90% of all the turkeys is predicted to be taller than 79.37 % of them.
The average height for turkeys at the 90th percentile for weight is 34.554
Of the turkeys at the 90th percentile for weight, roughly the percentage that would be taller than 28 inches 79.37%
Explanation:
The data given for the study can be listed as follows
For a population of turkeys at a farm, the correlation found between the weights and heights of turkeys is r = 0.64
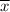 = 17 (i . e the average weight in pounds)
= 17 (i . e the average weight in pounds)
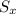 = 5 ( i . e the standard deviation of the weight in pounds)
= 5 ( i . e the standard deviation of the weight in pounds)
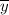 = 28 (i . e the average height in inches)
= 28 (i . e the average height in inches)
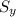 = 8 ( i . e the standard deviation of the height in inches)
= 8 ( i . e the standard deviation of the height in inches)
The slope of the regression line can be expressed as :
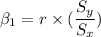
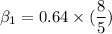
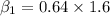
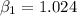
Similarly the intercept of the regression line can be estimated by using the formula:

replacing the values, we have:


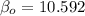
However, the regression line needed for this study can be computed as:
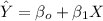
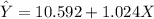
Recall that;
both the weight and height roughly follow the normal curve
Thus, the weight related to 90th percentile can be determined as shown below.
Using the Excel Function at 90th percentile, which can be computed as:
(=Normsinv (0.90) ; we have the desired value of 1.28
∴
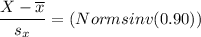
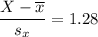
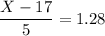
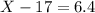
X = 6.4 + 17
X = 23.4
The predicted height
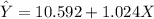
here; X = 23.4
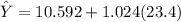

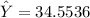
So the probability of predicted height less than 34.5536 can be expressed as:

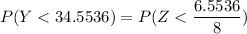
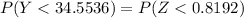
From the Z tables;
P(Y < 34.5536) =0.7937
Thus, a turkey at the farm which weighs more than 90% of all the turkeys is predicted to be taller than 79.37 % of them.
The average height for turkeys at the 90th percentile for weight is :
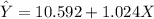
here; X = 23.4
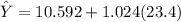

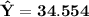
Of the turkeys at the 90th percentile for weight, roughly what percent would you estimate to be taller than 28 inches?
This implies that :
P(Y >28) = 1 - P (Y< 28)
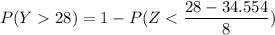
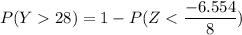
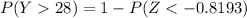
From the Z tables,


= 79.37%