Answer:
height of cliff (h) = 112.38m
Step-by-step explanation:
The time 5.12 s is the total time it takes for the rock to fall, and for the soundwave to travel back to the top of the cliff before it is heard.
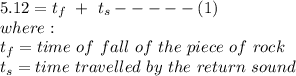
Let h be the height of the cliff in meters, the time taken for the rock to fall is given by:
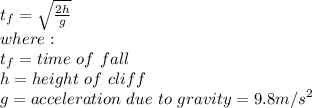
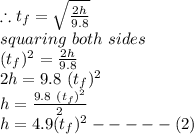
Next, let us calculate the time taken fot the sound to return

now putting the values of h from equation 2 into equation (3)
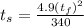
Putting the value of
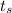 into equation (1)
into equation (1)
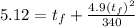
multiplying through by 340
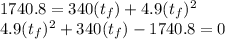
now let us solve the quadratic equationsss;
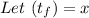

note, time cannot be negative, so we ignored the negative answer
putting the value of
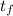 into equation (2) to find height of cliff (h)
into equation (2) to find height of cliff (h)
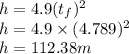
Therefore, height of cliff (h) = 112.38m