Question

A rock is dropped from a sea cliff and the sound of it striking the ocean is heard 5.12 s later. If the speed of sound is 340 m/s, how high is the cliff

Answer 1

height of cliff (h) = 112.38m

Step-by-step explanation:

The time 5.12 s is the total time it takes for the rock to fall, and for the soundwave to travel back to the top of the cliff before it is heard.

`5.12 = t_f\ +\ t_s - - - - -(1)\\where:\\t_f = time\ of\ fall\ of\ the\ piece\ of\ rock\\t_s = time\ travelled\ by\ the\ return\ sound`

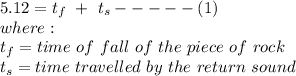
Let h be the height of the cliff in meters, the time taken for the rock to fall is given by:

`t_f=\sqrt{(2h)/(g) } \\where:\\t_f = time\ of\ fall\\h = height\ of\ cliff\\g= acceleration\ due\ to\ gravity= 9.8 m \slash s^2`

`\therefore t_f = \sqrt{(2h)/(9.8)} \\squaring\ both\ sides\\(t_f)^2 = (2h)/(9.8)\\ 2h = 9.8 *s\ (t_f)^2\\h = (9.8 *s\ (t_f)^2)/(2) \\h= 4.9(t_f)^2 - - - - - (2)`

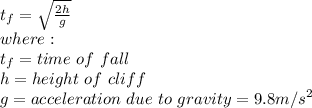
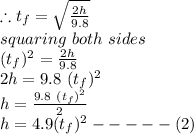
Next, let us calculate the time taken fot the sound to return

`t_s = (h)/(v) \\where:\\t_s = time\ for\ sound\ to\ travel\ up\ the\ cliff\\h= distance\ tavelled\ = height\ of\ cliff\\v= speed\ = 340m \slash s\ (speed\ of\ sound)\\\therefore t_s = (h)/(340) - - - - - (3)\\`

now putting the values of h from equation 2 into equation (3)

`t_s = (4.9(t_f)^2)/(340)`

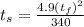
Putting the value of
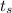`t_s` into equation (1)

`5.12 = t_f +(4.9(t_f)^2)/(340) \\`

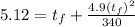
multiplying through by 340

`1740.8 = 340(t_f) + 4.9(t_f)^2\\4.9(t_f)^2 + 340 (t_f) - 1740.8 = 0`

now let us solve the quadratic equationsss;

`Let\ (t_f) = x`

`4.9x^2 + 340x - 1740.8 = 0\\using\ quadratic\ formula\\x = (-b \pm√(b^2 - 4ac) )/(2a) \\x = (-340 \pm√((340)^2 -\ 4 *4.9 *(-1740.8)) )/(2*4.9)\\x = (-340\ \pm\ 386.936)/(9.8) \\x =(386.938 - 340)/(9.8) \\x = (46.936)/(9.8)\\ x = 4.789\\x = t_f\\t_f=4.789s`

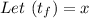
note, time cannot be negative, so we ignored the negative answer

putting the value of
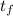`t_f` into equation (2) to find height of cliff (h)

`h= 4.9(t_f)^2\\h = 4.9 *(4.789)^2\\h = 112.38m`

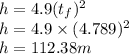
Therefore, height of cliff (h) = 112.38m