Answer:
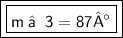
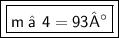
Explanation:
We know that the sum of supplementary angle adds up to 180 °
So,
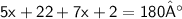
Collect like terms
⇒
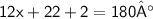
Add the numbers
⇒
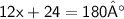
Move 24 to right hand side and change it's sign
⇒
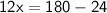
Subtract 24 from 180
⇒
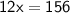
Divide both sides of the equation by 12
⇒
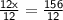
Calculate
⇒
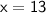
Value of x = 13
Now, substituting / Replacing the value of x

⇒
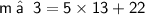
⇒
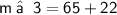
⇒
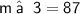
Again,

⇒
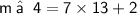
⇒
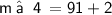
⇒
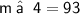
m ∠ 3 = 87
m ∠ 4 = 93
Hope I helped!
Best regards!!