Question

Find the measure of each angle: ∠3 and ∠4 are supplementary. m∠3 = 5x + 22 and m∠4 = 7x + 2.

Answer 1

`\boxed{ \bold{ \boxed{ \sf{ m \: ∠ \: 3 = 87 °}}}}`

`\boxed{ \bold{\boxed{ \sf{m \: ∠4 = 93 °}}}}`

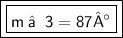
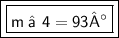
Explanation:

We know that the sum of supplementary angle adds up to 180 °

So,

`\sf{5x + 22 + 7x + 2 = 180°}`

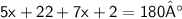
Collect like terms

⇒
`\sf{12x + 22 + 2 = 180°}`

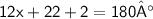
Add the numbers

⇒
`\sf{12x + 24 = 180°}`

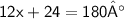
Move 24 to right hand side and change it's sign

⇒
`\sf{12x = 180 - 24}`

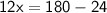
Subtract 24 from 180

⇒
`\sf{12x = 156}`

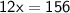
Divide both sides of the equation by 12

⇒
`\sf{ (12x)/(12) = (156)/(12) }`

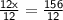
Calculate

⇒
`\sf{x = 13}`

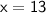
Value of x = 13

Now, substituting / Replacing the value of x

`\sf{m ∠ 3 = 5x + 22}`

⇒
`\sf{ m \: ∠ \: 3 = 5 * 13 + 22}`

⇒
`\sf{m \: ∠ \: 3 = 65 + 22}`

⇒
`\sf{ \: m \: ∠ \: 3 = 87}`

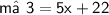
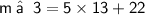
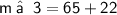
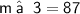
Again,

`\sf{ \: m \: ∠ \: 4 = 7x + 2 }`

⇒
`\sf{m \: ∠ \: 4 = 7 * 13 + 2}`

⇒
`\sf{ \: m \: ∠ \: 4 \: = 91 + 2 }`

⇒
`\sf{m \: ∠ \: 4 = 93 }`

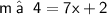
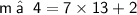
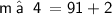
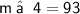
m ∠ 3 = 87

m ∠ 4 = 93

Hope I helped!

Best regards!!

Answer 2

∠3 = 87°

∠4 = 93°

Explanation:

Since ∠3 and ∠4 are supplementary it means the the sum of their angles is equal to 180°

To find the angles add both ∠3 and ∠4 and equate it to 180° solve for x and substitute it into their various expressions

That's

∠3 + ∠4 = 180

5x + 22 + 7x + 2 = 180

12x + 24 = 180°

12x = 180 - 24

12x = 156

Divide both sides by 12

x = 13

So for ∠3

∠3 = 5x + 22

∠3 = 5(13) + 22

= 65 + 22

∠3 = 87°

For ∠4

∠4 = 7x + 2

∠4 = 7(13) + 2

= 91 + 2

∠4 = 93°

We have the answers as

∠3 = 87°

∠4 = 93°

Hope this helps you