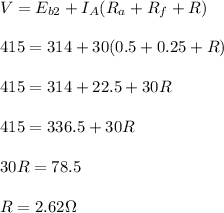Answer:
2.62 Ω
Step-by-step explanation:
For a series motor, the field resistance is in series with the armature resistance. The back emf (e) is given by:
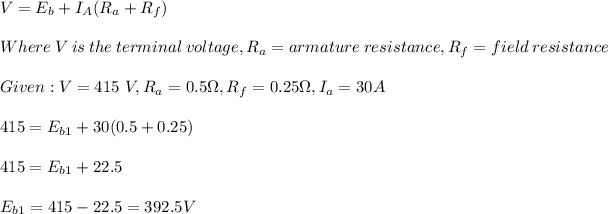
For a back emf of 392.5 V, the speed is 1000 rpm.
Speed is directly proportional to back emf. It is given as:
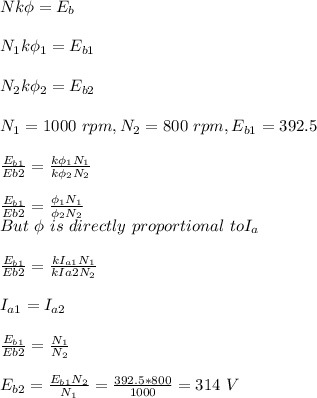
Let the added resistance be R