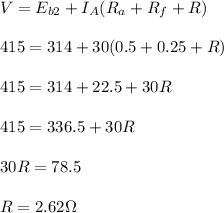Question

A series motor runs at 1000 r.P.M. When the voltage is 415 V and the current is 30 A. The armature resistance is 0.5Ω and the series field resistance is 0.25 Ω. Determine the resistance to be connected in series to reduce the speed to 800 r.P.M with the same current.

Answer 1

2.62 Ω

Step-by-step explanation:

For a series motor, the field resistance is in series with the armature resistance. The back emf (e) is given by:

`V=E_b+I_A(R_a+R_f)\\\\Where\ V\ is\ the\ terminal\ voltage, R_a=armature\ resistance,R_f=field \ resistance\\\\Given: V=415\ V,R_a=0.5 \Omega, R_f=0.25 \Omega,I_a=30A\\\\415=E_(b1)+30(0.5+0.25)\\\\415=E_(b1)+22.5\\\\E_(b1)=415-22.5=392.5V`

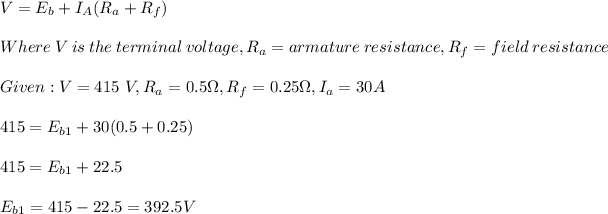
For a back emf of 392.5 V, the speed is 1000 rpm.

Speed is directly proportional to back emf. It is given as:

`Nk\phi=E_b\\\\N_1k\phi_1= E_(b1)\\\\N_2k\phi_2= E_(b2)\\\\N_1=1000\ rpm, N_2=800\ rpm, E_(b1)=392.5\\\\\frac{E_(b1)}{E{b2}}= (k\phi_1N_1)/(k\phi_2N_2)\\\\\frac{E_(b1)}{E{b2}}= (\phi_1N_1)/(\phi_2N_2)\\But\ \phi\ is\ directly\ proportional\ to I_a\\\\\frac{E_(b1)}{E{b2}}= \frac{kI_(a1)N_1}{kI{a2}N_2}\\\\I_(a1)=I_(a2)\\\\\frac{E_(b1)}{E{b2}}= (N_1)/(N_2)\\\\E_(b2)=(E_(b1)N_2)/(N_1)=(392.5*800)/(1000)=314\ V`

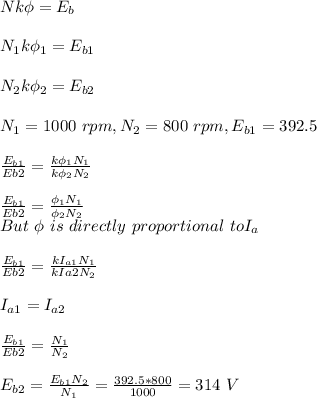
Let the added resistance be R

`V=E_(b2)+I_A(R_a+R_f+R)\\\\415=314+30(0.5+0.25+R)\\\\415=314+22.5+30R\\\\415=336.5+30R\\\\30R=78.5\\\\R=2.62\Omega`