Question

A rectangular channel 3 m wide carries 4 m3/s of water at a depth of 1.5 m. If an obstruction 15 cm high is placed across the channel, calculate the elevation of the water surface over the obstruction. What is the maximum height of the obstruction that will not cause a rise in the water surface upstream

Answer 1

the elevation of the water surface over the obstruction is highest at 1.341 m

the maximum height of the obstruction h = 0.159 m

Step-by-step explanation:

From the given information:

The diagrammatic expression for the water profile showing a rectangular channel with 3 cm width carrying a 4 m3/s of water at a depth of 1.5 m with an obstruction 15 cm high is placed across the channel can be seen in the diagram attached below.

To calculate the elevation of the water surface over the obstruction, we need to determine the following:

a. the velocity of the channel

b. the froude number at the upstream of the obstruction

c. the specific energy level

To start with the velocity V of the channel.

`V_1 = (Q)/(A) \\ \\ V_1 = (4 \ m^3/s)/((3 * 1.5 ) m^2 ) \\ \\ V_1 = (4 \ m^3/s)/(4.5 \ m^2)`

`V_1 = 0.88 \ m/sec`

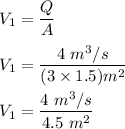
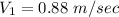
The froude number at the upstream of the obstruction

`F _(\zeta) = (V_1)/(√(gy__1))`

`F _(\zeta) = (0.88)/(√(9.81 * 1.5))`

`F _(\zeta) = (0.88)/(√(14.715))`

`F _(\zeta) = (0.88)/(3.836)`

`F _(\zeta) =0.229`

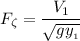
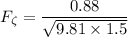
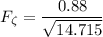
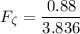
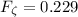
`F _(\zeta) \simeq0.3` which is less than the subcritical flow.

Similarly, the specific energy level for this process can be expressed as:

`E_1 = (V_1^2)/(2g)+y_1`

`E_1 = (0.88^2)/(2 * 9.81 )+1.5`

`E_1 = (0.7744)/(19.62 )+1.5`

`E_1 =0.039469+1.5`

`E_1 =1.539469`

`E_1 \simeq1.54 \ m`

`E_2 + \Delta z = E_1`

`E_2= E_1 - \Delta z`

`E_2= (1.54 - 0.15) \ m`

`E_2=1.39 \ m`

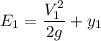
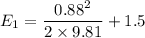
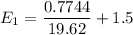
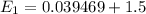
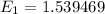
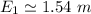
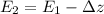
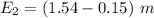
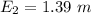
Suppose ;

`V_1 y_1 = V_2y_2\\ \\ Then; \ making \ V_2 \ the \ subject \ of \ the \formula\ we \ have: \\ \\ \\V_2 = (V_1 y_1)/(y_2) ---- (1)`

From the energy equation:

`E_2 + \Delta z = E_1`

we can now substitute the above derived parameter and have :

`E_2 + \Delta z=y_1 + (V_1^2)/(2g)`

`E_2 =y_1 + (V_1^2)/(2g) - \Delta z`

`E_2 =y_2 + (V_2^2)/(2g)`

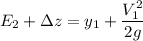
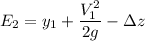
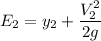
replace the value of
`V_2` =
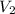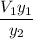`(V_1 y_1)/(y_2)` in equation (1), we have:

`E_2 =y_2 + (( (V_1y_1)/(y_2))^2)/(2g)`

`E_2 =y_2 + \frac{ {V_1^2y_1^2}}{2gy_2^2}`

`E_2 * y_2^2 =y^3_2 + \frac{ {V_1^2y_1^2}}{2g}`

`y^3_2 - E_2y^2_2 + (V_1^2y_1^2)/(2g)=0`

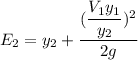
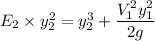
Replacing our values now; we have:

`y^3_2 - 1.39 * y^2_2 + (0.88^2 * 1.5^2)/(2 * 9.81)=0`

`y^3_2 - 1.39 * y^2_2 + (1.7424)/(19.62)=0`

`y^3_2 - 1.39 * y^2_2 + 0.0888=0`

`y^3_2 - 1.39 y^2_2 + 0.0888=0`

`y_2 = 1.341 \ m \\ \\ y_2 = - 0.232 \ m \\ \\ y_2 = 0.281 \ m`

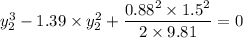
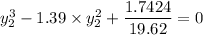
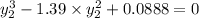
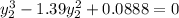
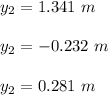
Therefore,the elevation of the water surface over the obstruction is highest at 1.341 m

What is the maximum height of the obstruction that will not cause a rise in the water surface upstream

In order to determine the maximum height , we need to first estimate the rise in water level surface of
`\Delta z`

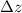
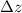`\Delta z` = 1.5 - (1.341+ 0.15) m

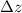`\Delta z` = (1.5 - 1.491) m

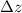`\Delta z` = 0.009 m

Finally, the maximum height of the obstruction h = (0.009 + 0.15 )m

the maximum height of the obstruction h = 0.159 m